Everything You Need To Know About Order Flow Auctions

- 1. Introduction
- 2. What is an Order Flow Auction?
- 3. The history of OFAs
- 4. Do we really need OFAs?
- 5. How to design an OFA: desired properties & architectural dimensions
- 6. Design Dimensions of an OFA
- 7. The Order Flow Auction landscape
- 8. Conclusion
Introduction
The capturing of Maximal Extractable Value ("MEV") usually comes at a cost to the end users of a protocol. Users might need to pay significantly higher prices for tokens and wait longer for transactions to be confirmed. This threatens the adoption of DeFi apps, as centralized alternatives are able to provide a better user experience.
One solution that has gained significant traction in the past year is Order Flow Auctions ("OFAs"). Users send their orders (transactions or intents) to a third-party auction, where MEV-extracting searchers pay for exclusive rights to run strategies on their orders. A significant portion of the proceeds in the auction are then paid back to the user, to compensate them for the value that they create.
We identified over 27 different OFA solutions, many of which have collected significant funding. The design space for these solutions is wide and teams have to make trade-offs between user welfare maximization, decentralization, and trustlessness, among others. We identify two main axes of differentiation between deployed/announced solutions. OFAs can be intent or transaction-based, and they can be specialized or general.
What is an Order Flow Auction?
Users interact with Ethereum in a way that allows sophisticated third parties to extract value from their interactions. We call this value Maximal Extractable Value or MEV (stay on the lookout for our forthcoming primer on MEV). Currently, most users get nothing in return for the value they create for third parties to feast on.
Let’s recap the usual lifecycle of a blockchain transaction on Ethereum to understand where the value that users generate is currently flowing.
Consider a user who wants to swap ETH for USDC.
- Step 1 - Intent expression: They express their intent to swap through a dApp front-end, which prepares calldata (which instructs the Ethereum Virtual Machine what to actually do) for a transaction.
- Step 2 - Transaction signing: The user signs this transaction using a wallet and sends it to the Ethereum mempool through an RPC endpoint.
- Step 3 - Searching: The mempool is constantly scanned by searchers looking for transactions that they can include in a bundle and send to a block builder.
- Step 4 - Block construction: The block builder collects bundles from multiple searchers and tries to create the most valuable block from the bundles sent to it and other transactions it has access to (e.g, simple transfers, transactions not included in a bundle by a searcher). The block builders send the blocks they assemble to the block proposer via a relay.
- Step 5 - Block proposal: The block proposer commits the most profitable block it receives and propagates it to other nodes in the Ethereum network.
Block builders must construct blocks using non-overlapping bundles. This means that if two or more bundles contain the same transaction (which is basically a guarantee for most opportunities), a builder can generally only choose one of them. Builders will thus usually choose to include the bundle that promises to pay it the most since that maximizes the amount that they can pay to the proposer for inclusion. This means that searchers will iteratively bid up the promised tip to the builder, even up to the point where most of the MEV is paid to them. [1]
The key takeaway here is that validators, who are just running the right software (MEV-boost), receive most of the value extracted. The searchers and builders who do the hard work of actually extracting the MEV often only get a small share (depending on the strategy) and the users creating the transactions get nothing.
Order flow auctions (“OFAs”) help us flip this dynamic on its head and compensate those at the beginning of the funnel (users, wallets and dApps) for the order flow they originate.
Informally, an OFA is a mechanism to pay back the users for the value that their transactions contain. It achieves this by selling user orders in an auction where searchers compete for the exclusive right to extract value from them. A portion of the auction revenues is then paid back to the users.
The user sends their transactions to the auction instead of the public mempool. The searcher bidding the most in the OFA wins the right to extract the MEV. One way to achieve this is to withhold full transaction data until the transaction has been sold. This would mean that only one searcher could submit a bundle with the auctioned transaction to a block builder.
Where previously searchers had to tip the validator to secure a placement in a block, now, since no other searcher has the same transaction, they can bid the minimum to be included in a block and still extract the MEV. This does not mean that the searcher profits more, the competition just happens at the OFA level, with the profits being competed away at the benefit of the order seller. With OFAs, validators receive less MEV, and a portion of those profits flows back to the user.
Now that we have a high-level understanding of OFAs and their purpose, let's approach this more formally.
TLDR: As the name implies, an OFA is an auction. Therefore, there must be a seller, a buyer, and an auctioneer.
- The auctioneers are the OFA platforms.
- The sellers are the order flow originators (dApps, Wallets, users).
- The buyers are the searchers/bidders.
What is being auctioned?
- Orders, that can be blockchain transactions or other arbitrary signed messages (i.e., intents, more on this later).
How do the transactions auctioned get added to the blockchain?
- Block builders connect to the OFAs & build the most valuable block available to them, hoping their one is the highest profit that the block proposer receives.
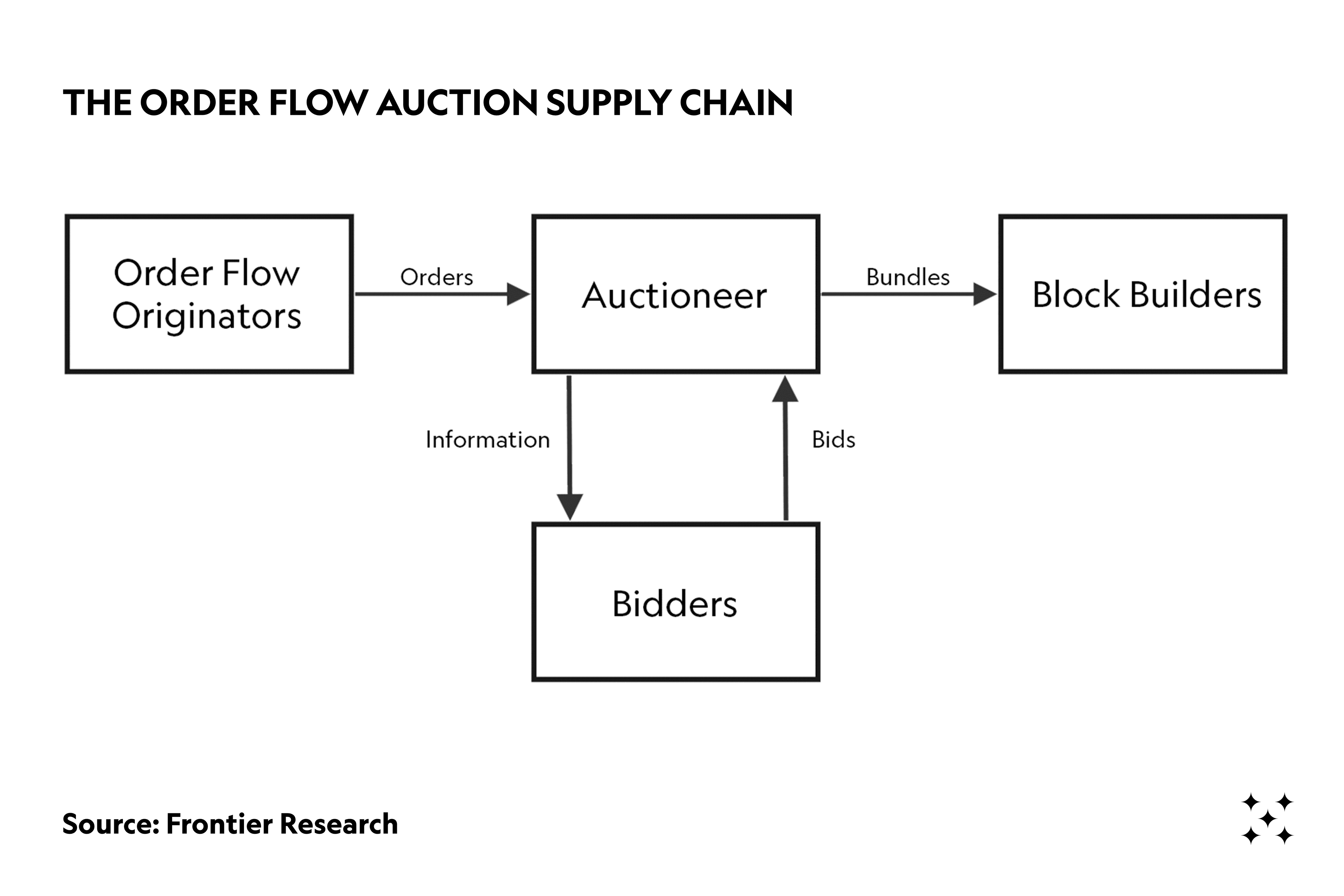
We refer to the framework proposed by Frontier Research to formalize the concept of OFAs. [2] Most OFA designs should have the following stakeholders, although some of the roles might be shared by the same entity through vertical integration (more on this later):
1. Order Flow Originators (“OFO”)
- OFOs are either the wallets, dApps or custodians that the users interact with to transact on-chain.
- Depending on the OFO used, the order is either a fully formed transaction or other cryptographic commitment (signed message/intent), which if executed allows access to the user’s funds on-chain.
- OFOs send the orders to a specific preselected order flow auction provider (auctioneer – see below). They are incentivized to send a specific order to only one OFA at a time (to maximise payout).
2. Auctioneer
- Receives orders from OFOs and holds the OFAs. The auctioneer will reveal varying degrees of information about the orders in the auction, and select the winner based on a predetermined winner selection function (like max rebate to the user, max fees paid, or best price offered).
- In some OFAs, the auctioneer forwards the winning bundle to the block builder directly, in others the winning bidder submits the bundle to its preferred block builder(s).
- If a user’s transaction contains no MEV and searchers do not bid for it, the auction still forwards the transaction to builders, or alternatively the public mempool.
3. Bidders
- Bidders will compete to buy the right to execute the transaction in the auction.
- They scan the orders on offer in the auction, simulate their strategies on orders they’re interested in, and submit bids according to their expected profits. In some auctions, bidders are also responsible for submitting the MEV bundles to the block builders instead of the auction.
4. Block builders [3]
- Receive the OFA bundles from either the auctioneer itself or the bidder who won the opportunity. Builders try to integrate with as many OFAs as possible to ensure they can build the most profitable block possible. Builders then build blocks combining order flow from OFAs with other sources the builder has access to.
- Note that inclusion by a block builder is only a guarantee of inclusion by the validator as long as that block is the most valuable proposed in that slot. This means that most auctions/bidders will submit to multiple block builders to try to minimize the time it takes for a transaction to land on-chain. We will dive deeper into block building and OFAs later in this post.
But how do these transactions on sale end up in the OFA in the first place? As the transaction lifecycle above denotes, historically users have sent their transactions blindly into the public mempool, unaware of the dangers they expose themselves to in the dark forest of Ethereum. Slightly more sophisticated users might have used a private RPC endpoint to send their transactions to specific block builders, hiding their transactions so that MEV searchers could not frontrun or sandwich them.
An OFA is essentially a more versatile version of a private RPC, and it mainly gets its flow through two avenues.
Firstly, most wallets allow users to manually edit the RPC endpoint that their transactions get routed to. A user aware of the dangers of MEV, who wants to get a kickback of the value that their transaction might contain, can select an OFA provider amongst the plethora of offerings available today and replace their wallet’s default RPC URL with the OFA’s. The main problem with this approach is that most users of crypto are completely unaware of the dangers of MEV, let alone the fact that they could monetize their order flow.
Therefore, the second (and more significant avenue) of order flow acquisition is exclusivity deals with wallets/dApps. The specifics of these agreements vary, but generally, the wallets agree to set a specific OFA as their default endpoint to submit transactions. In exchange for favouring one OFA provider, they get a share of the auction revenues, some of which they might pay back to the user. This means that if the user does not edit their RPC choice (if that is even enabled by the wallet), then all transactions will go through the OFA before inclusion on the blockchain. As an example, the Telegram trading bot Maestro, signed an exclusivity agreement with bloXroute to route their orderflow through their private RPC.
On the demand side, searchers are incentivized to integrate with as many OFA providers as possible, in order to have access to the highest amount of order flow and thus potential MEV to extract. Depending on the design of the OFAs, participating in the auction can be as simple as subscribing to a data feed but might also be limited to only a permissioned set of trusted/KYCed participants or might require the deployment of on-chain smart contracts. More on this in the section on OFA designs.
Readers aware of the crypto narratives du jour might have noticed that our initial definition refers specifically to the selling of exclusive access to transactions or the explicit sets of instructions that inform the EVM on how to achieve users’ goals. But this definition is limited, as it fails to cover many potential and existing types of OFAs.
Consider the transaction flow that we outlined at the start of this chapter, the process starts with the user having some intent about the state of the blockchain in the future. Currently, we get help from dApp frontends to turn that intent (e.g. “I have X ETH, and want at least Y USDC”) into a transaction.
Instead, we could directly express this intent as some signed message, giving some third party the right to formulate a transaction for us. We can similarly sell these signed messages in an auction. The winner of the intent auction is determined either by the highest bid or by most effectively meeting the user's needs.
Some limited intent-based systems already exist (e.g., CoWswap, 1inch Fusion, UniswapX) and will become more common in the future. More on the benefits of such systems at the end of this post.
Therefore, to be more general, we give the following definition:
An OFA is a mechanism for order flow originators to be compensated for the value that their intents contain by forcing sophisticated third parties to compete in an auction for the exclusive right to fulfil those intents.
It should now be clear that one of the major implications of OFAs is that MEV value re-distribution changes significantly. Most of the MEV profits get paid to the users instead of the validators.
We think this is a desirable outcome. Ideally, most of the auction revenue would be paid to the users who create these transactions to compensate them for selling their order flow and provide them with better execution by negating some of the negative externalities of MEV.
The history of OFAs
3.1 TradFi Origins - Payment for Order Flow
As with many things in crypto, some of the ideas around OFAs were explored in traditional finance before they made their way into the mind of crypto Twitter. For OFAs, the relevant TradFi parallel is payment for order flow (“PFOF”). PFOF is the compensation that brokerages receive for routing their clients’ trades to be executed by a particular market maker (“MM”)/liquidity provider. While mainstream awareness of PFOF increased after the retail trading boom and the emergence of commission-free trading, the topic has been explored since at least 1984 when the SEC mentioned it in a letter to the National Association of Securities Dealers (now FINRA). [4]
Why would market makers want to pay a pretty penny for the right to execute retail order flow? The main reason is a concept called order flow toxicity. [5] Simplifying, the more information that the trader has when submitting an order to a market maker, the more toxic their flow is. These traders use their informational advantage (alpha), to “pick off” mispriced quotes from market makers, which causes losses to the MMs. On the other hand, non-toxic, or uninformed flow is profitable to fill, because on average, the traders do not have an informational advantage, making it less likely that the market maker is trading at wrong prices.
So, the goal for the market maker is to try to source as much non-toxic volume as possible. The smartest traders, like hedge funds or prop trading firms, are generally not buying their Tesla calls from retail brokerages, so by paying to access flow from Robinhood, MMs can be more confident that executing against flow coming from them will generate a profit.
Does the user benefit from these dealings? While the jury seems to be somewhat out on this, research points to users generally benefitting from PFOF agreements. [6] One clear benefit is that the retail brokerages use some of the payments to cover execution costs for the users so that they can trade without fees. Secondly, users can benefit from better execution due to MMs being more comfortable quoting better prices to traders they know are less sophisticated than them.
On the other hand, best execution possible execution for the user is not necessarily guaranteed. In PFOF trades get routed to the MM that pays most to the brokerage, instead of the one promising the best execution for the trader. These two can be the same entity, but there is still a conflict of interest which is commonly cited in papers opposed to PFOF. [7]
To summarize, much like in traditional finance, in crypto, we also have parties interested in paying for user order flow because it is profitable for them. In fact, PFOF was the most common term used for the current crypto OFAs until late last year. The two terms do not exactly mean the same thing, though.
A fundamental difference is that in PFOF, the brokerage needs to find a counterparty to fill a user’s order (e.g. selling to a buyer). Crypto OFAs can be more expressive. We sell exclusive access to an order (transaction or intent), which depending on the OFA, can give the winner the right to do more than just fill a trade. In fact, in the current paradigm, transactions already define the counterparty, say an AMM liquidity pool, that the user will transact with. In this case, the searcher is just bidding to extract some of the value leakages that are inherent in our current dApps rather than to fill the order (with the caveat of JIT LPing [8]). If we move towards an intents/RFQ-based paradigm, we will see more searchers actually also act as market makers, as is the case with solvers on CoWswap or market makers on aggregators like 1inch or 0x. More on this later.
Another distinction is that OFAs can be fundamentally more open than TradFi PFOF. In TradFi, retail brokerages will sell access to order flow only to specific sophisticated market makers, like Citadel, SIG or Virtu. The promise of crypto OFAs is that we can have credible mechanisms that allow for the democratization and permissionless of access to orders. This means that anyone from Citadel to a 13-year-old can bid in the auction for user orders. However, this is not a guarantee – some OFAs will optimize for different properties, which might result in similarly concentrated markets as we see in TradFi – more on this later.
Finally, users in crypto have much more control over where their orderflow gets routed to. In PFOF the brokerage makes the choice of counterparty and auction mechanism for the trader. In crypto OFAs, wallets might set defaults, but users can also choose to send their orders through a different OFA.
So, OFAs are an old TradFi concept that was ported into crypto. When did the first OFA protocols for crypto get built? We can identify two main “eras” of innovation in OFAs, the pre-merge and post-merge eras.
3.2 OFAs before the Merge
The publication of the “Flash Boys 2.0” [9] paper triggered community-wide discussions around MEV and its impact on user execution. The first iteration of solutions involved hiding user transactions from the mempool – this is effectively what we now call private RPCs.
BloXroute was the first to the game, releasing a private transaction service for DeFi traders paying for their platform. It sent transactions directly to selected mining pools, who promised to keep a transaction private until it was mined. This service was expanded to retail users when in November 2020, 1inch released a private transactions feature that sent user transactions to trusted miners, directly through their front-end. Other similar solutions were later deployed by Taichi and mistX.
Hiding transactions did not take full advantage of the value inherent to them, and sending to trusted parties did not even necessarily prevent frontrunning (because you’re trusting the miner or its integrated searchers not to do so).
The first solution that started to resemble the OFAs that we have today was KeeperDAO’s (later known as ROOK protocol) “Hiding Game”, launched in February 2021. Users would route their trades to the KeeperDAO MEV bots which would try to extract any MEV value available. This MEV would then be redistributed in the form of $ROOK amongst participants in the Rook ecosystem (searchers, LPs, integrated DeFi protocols) according to a share that was determined by the protocol. Users could claim the rewards once per epoch (24 hours).
Bloxroute expanded its private transaction service to offer kickbacks by releasing BackRunMe in May 2021. By submitting transactions to the bloXroute RPC, a user would agree to their transaction potentially being backrun by a searcher in exchange for a 40% share of the MEV extracted. The searcher that was able to extract the most profit would be given the right to have their transaction included immediately after the user transaction (by miners that BackRunMe was integrated with).
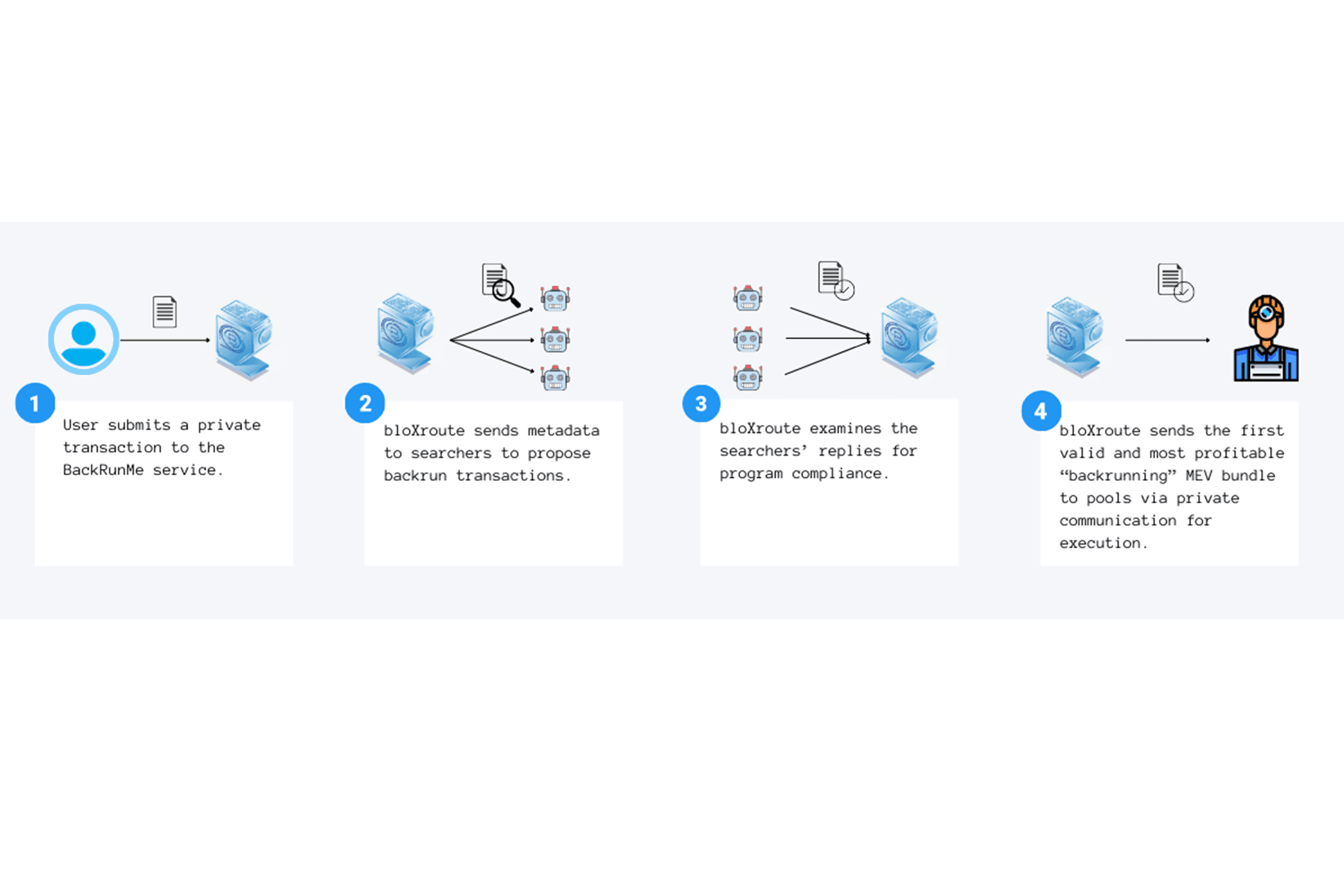
The big difference between these two was that Rook hid transactions by wrapping orders in a way that only allowed Keepers that KeeperDAO had whitelisted to extract value. This also meant that users had to either use the custom trading app by KeeperDAO or a DeFi protocol integrated with them to benefit from the protection. BackRunMe theoretically supported all protocols on Ethereum by running an auction for the user transactions through an RPC (theoretically, since coverage depends on what strategies the integrated searchers were running), but it also initially required users to register with bloXroute to use the service.
In June 2021, ArcherSwap (now Eden Network), also released a product that promised users some refunds from their MEV. ArcherDAO ran bots that would extract MEV out of their user’s trades. This profit would go back to the DAO and be used to buy $ARCH tokens from the market, these tokens would in turn be redistributed back to users that had traded on the platform. Other MEV cashback or gas-free trading protocols were released in 2021 by mistX & OpenMEV.
Another significant protocol launch around this time was CoWswap, which was initially launched as Gnosis Protocol in April 2021 and spun out of Gnosis in March 2022. CoWswap was one of the earliest implementations of an intent-based swapping protocol/OFA, where users would sign an intent to trade, which would allow third-party “solvers” to compete for the right to settle the user's order. The user's transactions did not hit the mempool, protecting them from MEV. Users were compensated for their flow in the form of better prices.
Even though MEV extraction was at its then highest-ever levels during the 2021 bull market, the previous solutions did not achieve significant adoption in the market. The dark forest had not yet been illuminated, and most users were (and still are) oblivious to the perils of MEV. The market was not yet controlled by any single player and seemed ripe for the taking, but users were slow to adopt MEV protection.
3.3 Order Flow Auctions after the Merge
The merge, with its move to proposer-builder separation (“PBS”) through MEV-Boost, reinvigorated the discussion around OFAs and acted as the catalyst for the second wave of solutions popping up. PBS was meant to reduce centralization at the consensus layer, by separating the roles of block construction and proposing.
PBS is certainly successful at addressing centralization at the consensus level, allowing even the smallest validators access to the most sophisticated and profitable blocks. But it did not remove all centralization vectors, rather pushed them to the block-building layer, where sourcing exclusive order flow proved to be the main competitive advantage for block builders vying for a share of the pie.
Given the increased importance of sourcing exclusive order flow and a market opportunity that had not yet been filled, a new wave of OFAs started to enter the market. Following the example of BackRunMe, similar simple OFA architectures (generalized transaction auctions, see section 7), started to be announced in late 2022, including the likes of Blink Labs, Wallchain, Kolibrio and others.
Worried about the centralizing effects of OFAs through exclusive order flow (more on this later), Flashbots outlined the design for SUAVE in November 2022. [10] It is an extremely ambitious project with the aim to create a decentralized block builder which will also include an auction for user intents. The release of SUAVE will take some time, but in the interim, Flashbots released their own OFA, MEV-share, in February 2023. It is built around the concept of programmable privacy, where users and order flow originators can choose how much information about their transactions they reveal to the bidders in the auction. We will dive deeper into why this is important later. Here, it is enough to understand that this helps with enabling permissionless access to order flow and protecting users from frontrunning.
Due to their higher versatility and potential for higher user welfare (more on this later), intent-based OFAs, similar to CoWswap, focusing on user execution improvement have been on the rise recently. DFLow was the first to follow CoWswap, being first announced in March 2022, with 1inch Fusion being released in December 2022, and most recently UniswapX in July 2023.
Given the number of solutions announced/deployed so far, the market is starting to look somewhat saturated. As of July 2023, 1 in 10 Ethereum transactions is sent through private mempools, either through an OFA or a private RPC. [11] The main limiting factor to OFA adoption is still the lack of awareness, but as wallets, or more familiar dApps like Uniswap adopt OFAs, we can expect this number to rise significantly. This race for order flow is likely to have only a few main winners. It remains to be seen whether the first movers will emerge as the victors, or whether newer protocols can find better designs in the vast OFA design space (which we will analyze in section 6).
Do we really need OFAs?
4.1 Why is MEV mitigation difficult?
The general approach to reducing the negative effects of MEV in Ethereum is two-pronged. Firstly, we want to reduce the total amount of MEV that exists and secondly, for the MEV that remains, we want to democratize extraction and redistribute the rewards more fairly.
OFAs fall into the latter category of solutions. They do not address the fundamental causes of MEV but create mechanisms that redistribute value back to those that originate it.
Why should we re-distribute rather than mitigate MEV? Could we not just try to get rid of it altogether at the application and protocol layer instead of building ad-hoc solutions that further complicate the transaction supply chain?
The short answer is yes, but it is hard.
Currently, the most common MEV strategies are CEX-DEX and DEX-DEX arbitrages, sandwiching, and liquidations. How would we go about addressing each at the application level?
Data from EigenPhi estimates the size of the DEX-DEX opportunity to have been 48% (or $145M) of the on-chain MEV opportunity in 2022.[12] Combining this with Frontier Research's lower bound estimate of $100M for CEX-DEX arbitrage for the same year [13], we see that these two types of MEV account for the vast majority of MEV that exists today (~$250M vs. ~$150M for other types).[14]
Arbitrageurs provide a valuable service of keeping on-chain prices between different liquidity pools and off-chain venues in line with each other. What we really need to ask, is how much we should pay for this service and who should be the one footing the bill. The answer to this will determine whether DeFi can ever rival TradFi and CEXes in financial efficiency and become something more than degens playing a game of musical chairs on various animal-themed coins.
The size of the CEX-DEX opportunity today is explained by two main factors:
- 1. Prices on an AMM only move when someone makes a trade
- 2. Ethereum blocks get committed on-chain in 12-second intervals
Both make on-chain prices stale. Price discovery occurs on higher liquidity and frequency off-chain venues, meaning that DEX prices will always lag the most up-to-date price of an asset. The LPs are the ones paying the arbitrageurs to provide the service of updating the CEX price on-chain.
The measure for this cost is called loss-versus-rebalancing (“LVR”), presented in Milionis et al. 2022 [15]. Simply put, it is the loss that the LPs suffer due to selling to arbitrageurs at an outdated price compared to if they were able to update or rebalance their LP position according to the new CEX price.
Recall our earlier definition of toxic flow. LPs trading against these arbitrageurs is a perfect case of toxic flow, which we know will cause most LPs, especially unsophisticated ones, to be unprofitable in the long term.
One proposed solution to the LVR issue has been to reduce block times significantly from the current 12 seconds. In Milionis et al., 2023, [16], it was shown that lower block times reduce the probability that a profitable arbitrage exists within a block. There will always exist a price difference to CEXes but if block times are lower, the difference in price after each block will be smaller. This means that arbitrageurs are less likely to be profitable after fees are taken into account. Lowering block times would therefore reduce the size of the biggest MEV strategy, CEX-DEX arbitrage, and help with one of the biggest issues with AMMs today, LP profitability.
Unfortunately, this would represent a significant design choice that seems counter to the current Ethereum roadmap and would have significant implications for things like home staking.
Another proposed solution is to use oracles and force users to provide an update to the price at which LPs trade, reducing losses. One could also use dynamic fees in conjunction with oracles to capture arbitrage losses for the LPs. [17]
While CEX-DEX arbitrage is a result of the difficulty of communicating between on-chain and off-chain venues, DEX-DEX arbitrage is fundamentally the result of bad order routing. If the price of a DEX pool after a trade deviates from other on-chain pools so much that even net of LP fees there is a profitable arbitrage available, the trade should have been split up across multiple pools. In this case, any backrun arbitrage profits that the searcher extracts could have been redistributed to the user as better execution.
In fact, the solutions to this form of MEV already exist, handling execution through aggregators or allowing a sophisticated third party to source the liquidity through multiple on-chain sources, like on CoWswap or what SUAVE is aiming to support.
Sandwiching represents the second highest volume MEV strategy after arbitrages. Users are exposed to sandwiching purely due to the parameters in the swaps they submit to DEXes. Setting too high a slippage tolerance means that a searcher can frontrun a user by buying a token before their buy and then selling immediately after the user to make a profit on the price change caused by the user’s trade.
There are many outlined solutions to reducing users’ exposure to sandwiching:
1. Hiding the transactions from searchers
- If the searchers cannot see the transactions before they are confirmed on-chain, then the user cannot realistically be sandwiched. Naturally, one way to achieve this is to avoid sending transactions through the public mempool, either through an OFA (that bans sandwiching) or a private RPC.
- If one does not want to trust the searchers in an OFA or block builders that receive the orders, encrypting transactions is one way to avoid sandwiching. One major roadblock for encryption as a solution is a decrease in UX due to latency and the required trust assumptions for things like threshold encryption or trusted execution environments. Shutter Network is one project working on this, and outside Ethereum we see teams like Osmosis and Penumbra building private transactions.
- Privacy as a solution is also applicable to other forms of MEV where extraction strategies involve a frontrunning component, like JIT LPing or generalized front running.
2. Setting better-informed slippage tolerances.
- Sandwiching is only really possible because users tolerate significant price changes when they are trading on DEXes. On low-liquid and volatile tokens, this can be even in line with user expectations, as speculative mania often makes users want to buy at any price. In other cases, it is just another symptom of users not understanding what MEV is and how a poorly set slippage tolerance gives free money to searchers.
- Therefore, applications can set slippage tolerances better. DEXes can adjust slippage tolerances dynamically based on statistical patterns, mempool state, volatility of the pool, or oracle prices. While doing this, the DEX has to strike a delicate balance between avoiding leaving room for sandwich bots and ensuring that user transactions do not revert
- A solution implemented by 0x, “Slippage Protection”, takes into account statistical patterns of slippage, when trading with specific pools, to optimize order routing and minimize the slippage suffered. [18]
3. Batch execution or singular price per block
- Sandwiching relies on orders within a block being executed at different prices. One could require that all orders within a block settle at a specific price, which ensures that no one trading in the same pool gets executed at a better or worse price than anyone else, leaving no opportunity for sandwiching. CoWswap is one protocol that currently has currently implemented this.
- Liquidations are another significant MEV frontier that we can address with application-level changes.
- When a lending position crosses the liquidation threshold, MEV searchers compete for the right to liquidate a position, which involves buying the underlying collateral at a discount by repaying the loan and selling the acquired collateral for profit within the same atomic bundle.
- Lending protocols usually pay a fixed liquidation bonus to the searchers to incentivize quick liquidations for positions that become too risky/unhealthy. But since this bonus is a fixed share of the collateral, in most cases it overpays the searcher for doing a relatively simple and commoditized strategy.
- To avoid this, newer protocols, like Euler Finance, have used Dutch auctions to gradually increase the bonus until some searcher is willing to execute the liquidation, which ensures that the protocol is not overpaying the searchers, thus reducing the size and impact of MEV on the users.
4.2 What types of MEV can OFAs address?
Now that we have inspected how we could mitigate MEV at the application level (per MEV strategy), let’s try to formalize a framework to reason about MEV mitigation. Are there specific MEV vectors that seem particularly nebulous, and hard to address?
Frontier Research’s excellent article “A New Game In Town” [19], presents a high-level framework for reasoning about different types of MEV. In the article, the MEV available from a transaction is split into two distinct types:
1. EV_ordering [20] refers to the value that can be extracted from transactions by purely reordering, inserting, and censoring transactions on a blockchain.
- This type of MEV does not require any risk-taking or information outside of the blockchain, meaning that if the searcher gets their bundle/strategy included in a block by a validator, they are guaranteed to make a profit.
- MEV strategies that fall under this category are DEX arbitrages, sandwiching and liquidations.
2. EV_signal refers to the value that can be extracted through strategies that reorder, insert and censor transactions on a blockchain in conjunction with some information, or signal, outside the blockchain’s state.
- The most common EV_signal strategy is CEX-DEX arbitraging, where a searcher executes an arbitrage non-atomically on both a centralized exchange and an on-chain decentralized exchange. The out-of-blockchain signal in this case is the price of an asset on a centralized exchange.
- The EV_signal of a specific transaction consists of both the value of the transaction as a leg of some strategy, like a CEX-DEX arb, and the informational value that the transaction provides. One example of the latter would be using transactions from certain wallets to predict the prices of an NFT in the future.
- Note that EV_signal depends on the utility function of the searcher. Certain transactions have EV_signal value only for certain market participants. This is because only certain sophisticated searchers can be competitive in CEX-DEX arbitraging, which requires low latency and fee tiers on a CEX, access to a block builder, the ability to warehouse inventory across multiple venues and to take on risk when competing for opportunities. This scale and sophistication advantage is a major contributor to centralization in the MEV supply chain, more on this later.
- This is contrary to EV_ordering, where most searchers will arrive at the same value since access to the strategies is commoditized (code up a searcher and bid better than your competition) and trading requires almost no capital (due to flash loans).
Let’s consider the previous analysis of solutions to address MEV at the application level. It seems like the solutions for EV_ordering, like better order routing, hiding transactions and Dutch auctions, are easier for us to implement than the ones related to EV_signal.
This makes sense, as EV_ordering only concerns itself with the current state of the blockchain and how including transactions in specific types of bundles alters it. With better application design, we will be able to create transactions that leave less room for this kind of atomic MEV to exist.
EV_signal strategies will be harder to completely remove even if we come up with better designs because, by definition, their value relies on information that is not contained within the blockchain. [21]
Even though applications might be able to estimate the EV_signal value of certain transactions, it is likely that these estimates will not be fully accurate. It is also unlikely that a dApp would be able to extract as much EV_signal as the most informed searcher. The best searchers have a competitive advantage, for example, lower fee tiers and latency on CEXes. Even with protocol-level changes, it seems unfeasible to get rid of the informational value of some transactions (like whales selling their holdings). As long as that is the case, it makes sense to have some mechanism to sell access to and redistribute that value.
This means that no matter how hard we try, there is likely to always be residual MEV that we cannot eliminate, either due to theoretical constraints or due to the trade-offs for doing so being too steep.
It seems that solutions to address EV_ordering exist, and we seem to have some ideas on how to reduce the impact of EV_signal so… why are users still suffering from MEV and do we still need OFAs?
As with many things in tech, sophisticated solutions mean nothing without distribution. Unfortunately, most of the existing protocols have sticky user bases, most of whom are not even aware of the MEV they expose themselves to. While a new application might be better at reducing its MEV exposure, onboarding both users and potential LPs to a completely new protocol and front-end is a significant challenge. [22]
While we might expect applications to address their MEV exposure through better designs in the long term, we will still need a solution in the short-to-medium term that can address the negative externalities of MEV without requiring significant user behaviour change.
In fact, it is the ease of adoption that makes OFAs a very powerful solution for MEV mitigation. Getting MEV rebates or protection as a user can be as simple as using a wallet which sends their flow directly to an OFA (or just changing the URL of the RPC endpoint in a wallet’s settings).
But are OFAs a good enough solution in the interim? Fundamentally, we want to build solutions that give users the best possible execution. We run an auction, instead of say making users sell their own transactions because users are not able to value their transactions as well as sophisticated third parties specialized in value extraction.
OFAs achieve best execution for users because rational bidders in competitive auctions will end up bidding close to the true MEV, the sum of EV_ordering and EV_signal, of a transaction. We see this game play out in the searcher marketplace for the most competitive opportunities, and we saw this game play out in the priority gas auctions (PGAs) [23] that settled MEV before PBS was introduced. OFAs reintroduce the same iterative process of searchers seeking alpha from transactions, getting closer to the true MEV of that transaction and bidding away most of the profits in competition against each other. The competition just happens in a different venue and the main benefactor is the user, not the validators.
We will further explore this later, but it is somewhat reductive to think about OFAs as mere tools for mitigating MEV.
We can think of OFAs as counterparty discovery for users seeking the best execution for their orders. OFAs, due to their position in the transaction supply chain, are primed to benefit from a move to more intent-based applications – using MEV mitigation as a user acquisition feature, while providing services like coincidence of wants or order route optimization for orders sent through them.
To summarize, OFAs mitigate the negative externalities of MEV extraction relatively easily without forcing users to change the applications they use. Even though it is likely that a significant amount of MEV will be reduced through application-level design improvements in the long term, there is also likely to be remaining MEV that can be redistributed via the use of OFAs.
How to design an OFA: desired properties & architectural dimensions
Designing OFAs seems quite simple: just build an auction whose winners get to exclusively execute user orders and pay the users/originators for the flow.
Unfortunately, auctions are never quite that easy. That we have a whole subfield of economics, auction theory, whose Nobel laureates are contracted by the US government to design wireless spectrum auctions should serve as a testament to that. [24]
Thus, it should come as no surprise that there has been a diverse set of OFA designs proposed and built. It is important to understand the different design dimensions of OFAs since even seemingly insignificant differences in design choices can have large effects on how the market dynamics of the OFA develop.
Before we analyze the exact design dimensions of OFAs, it will be useful to determine some of the desired properties [25] that we would like to have.
Considering the potential benefits for end users, OFAs could end up touching the majority of transactions that end up on-chain. We think the must-haves for OFAs are:
- 1. Maximizing user welfare
- 2. Robustness
- 3. Trust-minimization
It is also important for an OFA to 4. not significantly further the centralization of the MEV supply chain and 5. to be easy to use.
5.1 Maximizing user welfare
The main goal of an OFA should be to optimize for the welfare of the order flow originators. As described before, this can be in the form of a direct rebate as a payment for the order flow, or alternatively better execution, e.g. better price for a swap, the minimization of gas fees or optimization of other parameters that can be defined in the auction.
There are three major contributors to the welfare of someone using an OFA:
- 1. Execution improvement/rebate payments,
- 2. Speed and rate of inclusion
- 3. Competitiveness of the OFA.
Thus, the value that we want to optimize for can be defined as , where U is the utility function of the user that depends on how the user's intent or transaction is executed on-chain by the winning bidder of the auction. In addition to things like price, utility depends on the speed and certainty of inclusion. The design of the OFA has significant implications on whether the user welfare increase is in the form of a direct rebate or some improvement in the outcome, more on this in the next section.
Optimizing for user welfare is not simple because most of the value that is paid back to the originator is taken from the validator. OFAs present a constrained optimization problem, where the more that is paid to the originator, the less likely inclusion becomes in the next block.
This is because the winning bidder would contribute less to the value of the block it is included in (if it even gets included). If the OFA only submits to select block builders, there is a chance that the proposing validator will have access to a more valuable block, which does not include transactions from this OFA. This becomes an even larger problem as order flow gets fragmented to multiple different OFAs, each potentially submitting to non-overlapping sets of builders, meaning that user orders compete against each other for inclusion, which further drives down the rebate.
For UX purposes, bidders participating in the auction should provide some sort of credible commitment to the user that their transaction will end up on-chain. Users should be confident that the transactions they submit through OFAs will eventually make it on-chain. There are multiple solutions to this (each with its own drawbacks), including forcing bidders to pay the users even if they don’t get included (non-contingent fees), slashing penalties or a reputation system.
The chance of eventually being included in a block is important for UX but so is the latency of inclusion. As a rule of thumb, one can estimate the average time for inclusion by taking the inverse of the total market share of the builders the OFA is integrated with, or which the searcher submits to. If a bundle is submitted to builders whose cumulative share of the builder market is 50%, one can expect to get executed within 2 blocks.
All block builders are not created equal, though. During volatile times, searcher-builders win blocks significantly more often due to exclusive order flow, and most OFAs are wary of submitting to them, which means that inclusion time increases as markets get more volatile. The obvious solution seems to send orders to as many builders as possible – however, this increases (the chances of) value leakage (more on this later).
It is reasonable to assume that OF originators, like wallets, might optimize for inclusion rates rather than best execution/rebates when choosing which OFA to send their flow to as users are more likely to notice increased latency vs better execution, e.g. price impact. This can probably be addressed at the UI/wallet level though, by highlighting in each transaction pop-up how much better the execution was relative to non-OFA execution.
Since different users have different utilities for quick inclusion, OFAs can and do also allow the user to indicate their execution preferences, whether to optimize for speed of execution (send to everyone), maximize the expected welfare (send to only specific builders), or keep the transaction completely private from the bidders and send directly to a neutral builder.
Lastly, it is also very important that there is a competitive market both between OFAs and within a single OFA. If the rewards for the stakeholders, like searchers, to participate in the OFAs are pushed too thin, or the requirements to enter are too steep, there is a danger of only a few winners emerging. These winners can then further compound their advantages through economies of scale. In general, the fewer parties bidding, the higher the chance for collusion and rent-seeking behaviour, which comes at a cost to the user due to reduced auction revenues.
5.2 Robustness
OFAs must be robust to adversarial environments – they should assume their participants are constantly trying to find ways to exploit design choices for their gain. The systems we design should still achieve the other must-have properties, even if the participants cannot be assumed to act honestly all the time.
For example, OFAs need to decide on how they deal with the same entity bidding using multiple identities (Sybil bidders), how they counter spam bids and DOS attacks or whether auction participants can collude to extract profits. Each of these considerations plays into the decisions on how to design auctions, for example, combinatorial auctions (where one bids for collections of orders rather than just one) become difficult in the presence of Sybil bidders. [26]
OFA designers and users need to fully understand the vectors of attack and respective repercussions (e.g., can any OFA participants lose funds if the system fails to work as expected?).
5.3 Trust-minimization
Given that OFAs could potentially interact with most blockchain transactions, it is important that we build systems that require minimal trust in third parties. OFAs should guarantee that winners are selected fairly, that information is not leaked to privileged parties for their gain, and that any deviations from the promises the auction makes to its stakeholders can be noticed quickly.
Most of the OFAs currently deployed are compromising in this area as most auctions are run by opaque centralized entities.
One added complexity to designing trust-minimized OFAs is the number of different vectors for collusion. OFAs could extract rents by colluding with order flow originators, select searchers or block builders. The challenge is that in crypto users are not necessarily protected by things like best-execution regulations, so some market participants can, and do, do things that are in a legal grey zone. [27]
It’s important to highlight that the fear of collusion or other market-distorting behaviour is not unfounded. As an example, Google was recently sued by the DOJ for anti-competitive behaviour in their AdSense auction [28].
One possible way to minimize trust assumptions is to decentralize the auction. However, unfortunately, trust removal often comes at a cost. Decentralization potentially results in increased latency and lower computational efficiency. Furthermore, it introduces the need to provide economic incentives for the entities running the decentralized system.
Censorship is also another consideration when decentralizing auctions/having them on-chain, as long as block building is done by parties that might have the incentive and ability to do so. One solution proposed in Fox et al. (2023), is having multiple concurrent block proposers. [29]
For many OFA designs, the bottleneck for decentralization is still technological. The theoretical designs might exist but rely on technology that isn’t quite production-ready yet. This is denoted by how Flashbots has approached the development of MEV-share, where the plan is to progressively decentralize as encryption technologies mature.
5.4. Avoiding centralization in the MEV supply chain
As covered previously, the current MEV settlement infrastructure, built around proposer-builder separation (PBS), was created to alleviate the centralization pressures arising from MEV extraction at the validator level. What it did not do is get rid of the centralization vectors completely, just moved them from the consensus layer to the block-building layer.
So MEV is a centralizing force in both vanilla block proposing and PBS, but as we will see in the next section, the introduction of OFAs can further centralization at the block builder level due to exclusive order flow and informational asymmetry. If only searcher-builders will be able to win in the auction due to their informational edge or scale advantage, we end up trusting a few trading firms with the processing of a majority of the transactions on Ethereum.
We want to create designs that do not establish an oligopolistic market of a few winning builders or searchers. But this might be a tall order, given the parallels in TradFi, we might expect only a few entities to be competitive.
It is important to differentiate between a completely decentralized market, a centralized but contestable, and a centralized but uncontestable market. It might be that a market that has a few sophisticated centralized entities winning is acceptable as long as it can be realistically contested by other entrants (which is why we think this is a nice-to-have, not a must-have for OFAs). It might even be that a centralized market that is contestable results in better user welfare if the decentralized solutions have to make trade-offs with latency or expressivity.
5.5 Ease of use
Ideally, users don’t need to know of MEV/OFAs to benefit from MEV distribution. Currently, most OFAs require the user to manually change their RPC to the OFAs, but as the space matures, we expect wallets to sign deals with OFA providers to exclusively send their order flow to them, in which case no user behaviour change is required.
It is important that the friction for bidders to join the OFA is low to ensure the market is as competitive as possible.
Given the nascency of the field of solutions, we can expect both the searcher and user experiences to improve as designs mature and are battle-tested in production. Laminar, which aggregates and standardizes orders from multiple different OFAs, is a great example of solutions bridging the UX gap. [30]
Design Dimensions of an OFA
Next, we want to consider the different design choices that can be made when building an OFA, and how these choices affect how the OFA accomplishes each of the desired properties outlined in the previous section.
In this section, we cover the following dimensions:
- 1. Auction scope
- 2. Order types
- 3. Winner selection
- 4. Auction mechanism
- 5. Degree of information reveal
- 6. Access to order flow
- 7. Bidders
It is important to note that most of the dimensions are just that, a spectrum rather than a binary choice. This explains the plethora of different OFA solutions currently on the market, which we will dive deeper into in the next chapter.
6.1 Auction scope: generalized vs. app-specific OFAs
First things first, when building an OFA, one of the key things to decide on is the scope of the auctions.
We have two options:
- 1. Niche in and focus on single order types (usually swaps) potentially originated exclusively from a small set of applications (e.g. UniswapX)
- 2. Generalize and support multiple applications.
Generalized and app-specific auctions differ in the user welfare they generate, how that welfare is redistributed and, whether applications can use the OFA as a revenue stream.
Whether app-specific or generalized OFAs produce more welfare to the user is still up for debate.
The pro-specialization argument says that:
- 1. Users can be better compensated in the form of implicit execution improvement, which is also more efficient from a fee perspective.
- 2. Apps can vertically integrate by creating their own OFA and secure an extra revenue stream
- 3. Currently, most MEV is created by only one transaction type, swaps.
OFAs that focus on a specific type of order, like a swap, will find it easier to pay the user back in some form of implicit improvement in execution rather than a rebate transaction. This is because bidders in these auctions can specialize in filling only one order type, say swaps. The more order types are included, the more complex the auction becomes from the perspective of compensating users in terms of implicit improvement.
Implicit improvement is also more efficient from a fee perspective. To see this, let’s think about a backrun arbitrage. We have two trades, by the user and the searcher, both of which have to pay LP and gas fees. We also pay fees for the rebate transaction paid to the user for selling their transaction in an OFA. If the OFA compensation came in the form of a price improvement, there would only be one transaction, paying LP and gas fees only once.
Another advantage that specialized specific auctions have relative to generalized ones is that they can serve as an additional revenue source for dApps. In many OFAs, the auctioneer takes a cut of the revenues on offer as compensation for building and maintaining the service. If a dApp creates its own OFA and incentivizes sending flow from its app to that OFA, then they’re able to retain some value that would otherwise leak to the generalized auctioneer. As an example, the Uniswap Governance will have an ability to charge a fee of up to 0.05% from the output of each UniswapX transaction.
The pro-generalization argument is twofold:
- 1. OFAs want to maximize their potential addressable market
- 2. The whole can be larger than the sum of its parts (all single-order types). The more orders and order types in an auction the higher the chance of complementary order flow
There are cases where the searcher will be willing to bid more for two transactions in the same auction, due to complementary order flow, than for those transactions separately. As an example, a searcher could bid for an oracle update that would enable a liquidation, which in turn would create an arbitrage opportunity on some DEX pool. The searcher is willing to pay more in a general OFA, due to the certainty that winning a single auction provides, vs. having to potentially compete for these opportunities across multiple auctions.
It’s important to note that this also has a second-order effect: because OFAs benefit from a flywheel effect (the more orderflow, the better the execution, the more order flow,….) it is reasonable to assume that the market might see significant concentration, which is further exacerbated by the fact that OFAs generally operate under exclusivity agreements. Wallets will want to use the OFA that optimizes either their users' execution or provides them with the most cash flow. If complementary order flow makes each transaction in that auction more valuable, then wallets are more likely to choose a general OFA as their provider.
While it might be more efficient from a gas and blockspace perspective to provide better execution rather than paying rebates, it is worth considering the commercial implications of this decision. For the average user, rebates will be more easily noticeable than improved execution.
An analogous example from the real world is grocery rewards programs, where a customer might earn some points that they can use towards other purchases in some store. The customers could just instead go to a discount store without any loyalty programs and buy the goods for cheaper, but it feels better to accumulate some rewards than just pay a lower price.
6.2 Order Types: Transactions vs. Intents
OFAs need to decide whether the orders on auction are transactions or intents. Both types of orders represent some wish that a user has on the future state of a blockchain but differ in what kind of constraints they put on the execution of that wish.
Let’s consider a user with 10000 USDC that they want to swap for as much ETH as possible. We can represent this order as both an intent and a transaction.
A transaction in this case is a set of explicit instructions, or computational path, that transition the state of the Ethereum Virtual Machine to one where the user’s wishes are met. In our example, the transaction would explicitly specify which smart contracts need to be interacted with (e.g. Uniswap) and what data must be provided to them (e.g., how much the user is willing to trade, slippage tolerance).
An intent on the other hand would be a signed message sent to a third party, that instructs its receiver to work within certain constraints (e.g., net at least 5 ETH or fill the swap within the next 10 blocks) to create a transaction that achieves the goal specified in the intent (swap as much of my 10000 USDC to ETH as you can).
So, the difference is that in the first case, the user has already set the computational path that must be taken and there is very little that the winner of an auction can do to change the execution of the transaction. In the intent case, the third party, or the winner in the OFA, needs to craft a computational path and create a transaction that achieves the user's goals within the constraints provided.
In intent-based systems, participants in the auction need to be specialists in execution optimization. It is up to the bidders to formulate the explicit computational path, or blockchain transaction, that achieves the user's need, like swapping 10000 USDC to as much ETH as possible. The benefit here is that because the auctioneer can simulate the outcome of the proposed transactions, it can also select the winner of the auction to be the third party that achieves the largest optimization in execution rather than who bids the most.
All the currently released intent-based auctions allow only permissioned actors to execute user intents. This is because relative to transaction-based systems, users have to put a lot more trust to the solvers in intent-based auctions.
This is because the user gives relatively free reign for the solver to formulate transactions that achieve their intent. To protect users from malicious solvers, protocols like CoWswap require the solvers to bond a significant amount of value that can be slashed and paid back to victims in case of malicious or unintended behaviour.
Looking at the other desired properties of OFAs, intent-based auctions seem to further centralization in the MEV-supply chain as providing optimal execution will require a lot of sophistication, potentially even the willingness to take on risk (using active on-chain liquidity to match user orders) or to hedge positions accumulated on CEXes. It seems likely that intent auction participants integrated with block builders will be in an advantaged position. This is further exacerbated by the fact that, unless trust assumptions for the executors can be relaxed, access to the orders will be permissioned.
Interestingly, if we think about any intent-based architecture for a blockchain app, if the selection of the third party that gets the right to execute the user's intent happens through a competition to improve the user’s execution, then this architecture meets our definition of an OFA. Even though most of the currently deployed OFA protocols are transaction-based, as intent-based architectures become more common, so do intent-based OFAs.
Intent-based OFAs do not have to be completely general (e.g. SUAVE) and can instead focus on just a specific type of intent (e.g., CoWswap). More on this in the next section.
6.3 Winner Selection
OFAs need to make a choice about what auction type to implement, which price the winning bidder pays, first-price, second-price or maybe even a descending price (Dutch auction) and whether to make the bids public or private.
Each choice affects the auction’s competitive dynamics in subtle ways and limits the extent to which the auctions are resistant to different types of adversarial bidders or sellers. Most of the currently released OFAs are sealed-bid first-price auctions.
Fundamentally, we want to design systems that maximize user welfare. From our previous analysis, we know that selecting the bidder that promises the highest rebate might not achieve this because the inclusion rate might be decreased. So, the auction needs to decide whether to sell the order flow to the bidder which promises the validator the most or which promises the originator the most. Most OFAs seem to have chosen to impose a specific split of MEV back to the originator and the validator, anywhere from 40/60 to 90/10 (with a small fee potentially taken by the OFA itself), trying to find the sweet spot that maximizes utility as a function of inclusion rate and auction revenue.
Alternatively, the OFA could just let the free market decide the split, giving execution rights to the bidder that promises to pay the user the most. In this case, inclusion times could become a serious issue as the competitive market would probably drive the user refund near 99%, at which point the validator could often find more valuable transactions to include in the next block. This explains why currently only MEV-share seems to have allowed searchers to customize the split.
Intent-based OFAs need to consider different notions of a winning bid because there the competition can happen on the improvement in execution, not just the rebate, so the auction has to have a clear notion of what it means to achieve better execution. This will be easier in app-specific auctions, like swaps, where you can select the transaction bundle that achieved the best price.
6.4 Auction Mechanism: Per Order vs. Batch Auctions
Most OFA solutions in the market are per order, meaning that bidders bid on the right to execute specific orders. In a batch auction system, like CoWswap, the bids are submitted for the right to execute some batch of orders, e.g., all the orders going into the next block.
Batch auctions are better at uncovering the synergies of order flow thus potentially resulting in higher auction revenues. They are not as easy to implement and suffer from an attribution problem, though. If a bidder is paying a certain amount for a batch of orders, it is hard to say how much each order in the batch contributed to the value of that bid and therefore “fair” redistribution to the originators is harder.
An interesting variation of this is combinatorial auctions, where you are able to bid varying degrees based on a combination of different orders on offer. One could imagine a situation where an auction has orders A, B, and C on offer and a bidder has a strategy that he could extract value from only if he could execute on all three orders. In this case, a per-order auction would result in lower bids overall, because the bidder would have to take into account the risk of not winning the other two auctions. In a combinatorial auction, this preference could be expressed as a conditional bid, where the searcher would bid X for all three orders, but 0 for any other combination of them.
Robustness is not easy to achieve with combinatorial auctions. Just consider a case where one of the orders (say A) on auction was submitted by someone also bidding in the auction. If this entity wanted to have access to orders A and B, they could now bid higher than others for that same combination, because they will get a portion of the auction revenue (as they are selling one of the orders on auction). So, for a combinatorial auction to be robust and competitive, it needs to ensure that the same parties cannot be bidding and selling transactions, which might be difficult to achieve in crypto, at least without trade-offs.
6.5 Degree of Information Reveal: Private vs. Public Orders
OFAs must decide on how much information (about the orders) they reveal to the bidders. How much information gets revealed and to whom is important because the more information about the orders you provide, the more value from the transaction can leak outside the system.
Value leaks from the auction if users get frontrun by searchers but this is only possible if searchers are aware of the transaction in the first place.
Since we are selling the orders in an OFA, we could just not allow searchers to submit sandwich bundles, as a condition for participating in the auction. The first problem with this is that it introduces additional trust assumptions, but the bigger issue is that it might only fix frontrunning within a bundle. Block builders and searchers might still able to sandwich or frontrun users as part of other bundles included in the same block, before and after the targeted transaction or by using the information provided by the transaction trading on off-chain venues.
From section 4.2, we know that in a competitive auction, bidders bid close to the MEV of a transaction. This value is the sum of the EV_ordering and the EV_signal of that transaction. The goal of the bidders is to arrive at estimates for both of these values on each order they bid on. The less information that is shared about the order, the less confident the bidder can be about their bid being profitable, which likely leads to smaller revenues overall. Here it is likely that more sophisticated players who are able to take more risk will win more often in the OFA, potentially leading to further centralization in the MEV supply chain. One way to address this issue is to build an auction that enables the bids to be changed based on the contents of the orders (programmable bids), but this does not seem easy to achieve.
Let’s consider a concrete example to understand what kind of data can be hidden. Given an order to swap assets on Uniswap, a privacy-optimizing auction would potentially only reveal the pool that a user is trading in, but not the size or direction of the swap, making it impossible to sandwich if trust assumptions hold. A searcher could try to extract value here by submitting two orders, one buying and one selling, where one of the transactions would revert. Alternatively, the strategies can also be run on-chain, where the strategy triggers itself when the user transaction (and the information it contains), the input of the strategy, gets revealed.
One could also design auctions where only the winner has full access to the information of the order. This is valuable since some EV_signal strategies rely on certain information only being available to as few people as possible. We call this the exclusive informational value of a transaction. As an example, there might be a big pending sell order on a token one has exposure to. If this order was submitted to an OFA where every bidder had full access to this information, there would be no exclusive informational value, as every bidder could react even without winning the auction. If the full information of the order is given only to the winner, the bids could be higher, as they can take into account the exclusive informational value of the order (e.g., how much less you lose on a trade because you can hedge based on the information in the auction). On the other side, the searchers would have to bid based on some expected value model, with uncertainty that could reduce the auction revenues overall.
We could develop this idea even further. Instead of only revealing information about a single transaction to the winner of the auction, we could auction access to order flow for an entire block. The bidders in the auction would bid based on the expected value of the order flow. Because only the winner of the auction has access to the full information about the transactions, they can capture the maximum EV_signal (extraction and informational value) and EV_ordering (increased due to order flow synergies) available from that order flow.
Going back to our definition of user welfare (which we want to optimize for), on one hand, hiding information might make U(outcome) better because users are protected from frontrunning strategies, on the other, the less information the bidders have, the less they will bid (to avoid losses), which reduces the rebate paid.
It is also very important to understand the trust assumptions while using a privacy-enabling OFA. Orders going through an OFA will always have to be processed by some intermediary that runs the auction logic. The stakeholders in the auction will need to be confident that no information is being shared with any other participants for their gain. Because block builders need to see the contents of the transactions to build blocks the private auctions can only send to a trusted set of builders, contributing to centralization.
Solutions to this include forcing builders to commit some capital subject to slashing conditions (which could still limit the set of builders) or using trusted execution environments. Building a credible system that can enable some of these privacy functionalities without centralizing the MEV supply chain is one of the reasons SUAVE is in development.
Optimizing for privacy while ensuring that the system is credible requires quite complex designs, which can potentially limit the expressivity of privacy-focused OFAs in the short- to medium-term. Things like intent-based swap fills with active liquidity become much more difficult to achieve and the less information you provide to a market maker, the worse a price you will get.
6.6 Access to Order Flow: Permissionless vs. Permissioned
The OFA must decide who has access to the order flow that is on auction. The OFA can choose to offer anyone access to the order flow (e.g., through an API) or alternatively limit access to only specific approved parties. With most current designs, the OFA also has to choose which block builders have access to the flow.
Given that limiting the bidder set makes the auction less competitive, which results in less revenue and user welfare, why would an OFA want to limit the set of bidders?
There are a few potential reasons:
- 1. OFAs want to avoid value leakage
- 2. Permissioned/permissionless OFAs optimize for different trust assumptions
- 3. The ability to KYC the stakeholders in the auction.
A permissioned auction is able to credibly enforce its rules. Both the bidders and the block builders integrated with the OFA can, depending on the design, take advantage of their position at a cost to the user, e.g., by frontrunning or censoring users’ transactions.
If some stakeholders misuse their position in a permissioned OFA, they can be blocked from accessing the order flow. Any malicious actor would then have to weigh the potential losses in revenue, against the gain from acting maliciously. In addition to blocking access to future cash flows, the auction can require the bidders to bond some capital that can be slashed in case the bidders misbehave.
The problem with permissionless auctions is the fact that new identities are cheap, especially in crypto. If someone misbehaves, banning is not a credible solution because circumvention is trivial in an auction that allows anyone access. The auction will therefore either have to be permissioned or require no trust in the searcher’s behaviour.
Block builders are a trusted party within the MEV supply chain. They can unbundle searcher transactions, construct blocks that cause worse execution for users for their gain, share bundles sent to them with other parties or refuse to pay the auction rebate to the user. OFAs will attempt to provide users with certain guarantees regarding to how bidders/searchers can handle their transactions, promising not to accept bundles that frontrun or sandwich users, but this is hard to enforce at the block builder level. For this reason, it might make sense to work only with a limited set of builders that have committed to specific rules on how transactions should be handled (this is what we see in the market today).[29]
In addition to trust and user welfare considerations, regulatory concerns might play a role in deciding whether to limit access to the OFA. OFAs can act as a significant source of revenue for wallets and thus, depending on regulation some wallets will want to understand who their counterparties are. It is likely that US-based wallets would have to comply with OFAC regulations and would not be able to sell their order flow to sanctioned entities, which would require KYCing all the bidders/block builders participating in the auction (or alternatively segmenting bidders/originators, much like we do with OFAC compliant relays today).
One significant issue with OFAs limiting the set of bidders and the set of block builders they submit to is that it creates difficult barriers to entry. While technical challenges might make it difficult to achieve this right now, considering the significance of the solutions that are being built, we must ensure that there is a roadmap to reducing as many reputational and trust-based barriers to entry. Otherwise, permissioned access to order flow is just another way that OFAs contribute to the centralization of the MEV supply chain.
6.7 Bidders: Builder-Oriented vs. Searcher-Oriented OFAs
Another important consideration that affects the long-term dynamics of the OFA market is to whom the auction sells extraction rights. The most natural choice is existing searchers, but an OFA could just as well sell order flow directly to block builders who run searching strategies. We can thus divide the OFA space into two categories, searcher-oriented (“SOFAs”) and builder-oriented (“BOFAs”). [32]
All of the current OFA designs on the market are SOFAs. A SOFA gives access to searchers to bid on orders and the winning bundle is then submitted to a select group of block builders for inclusion (either by the searcher or by the OFA directly).
In the BOFA case, the bidders in the OFA are the block builders. The point of a BOFA is that the auction not only grants extraction rights of a transaction to the winning bidder but also guarantees that no other block builder will have access to that transaction. To understand why this is significant, recall that builders compete against each other to be chosen by the block proposer of that slot in the PBS auction. To win, a block builder needs to build the most valuable block given the transactions and bundles it has access to. The more transactions a builder has access to (relative to the other builders) the more likely that it can construct the most valuable block in that slot. Any source of exclusive order flow will therefore make you more competitive, more likely to land a block, and thus profit. The hypothesis is that because of this, builders are willing to pay more for order flow than searchers, which would result in higher auction revenues and thus potentially better welfare for the users.
Why would a builder pay more in a BOFA?
Builders can generate profit in two ways
- 1. On the difference between the tips it gets paid by the searchers and what it promises the validator
- 2. By running their own proprietary MEV strategies that extract value by inserting new transactions, reordering and merging bundles
We expect that in a competitive auction, the bidders will bid up to the MEV available in the bundle, the sum of EV_signal and EV_ordering. Block builders are willing to bid more than searchers, because each order that they have (in a BOFA) makes them more likely to win the next block, which makes them more likely to be able to extract MEV with their builder-searching strategies.
To formalize, the builder is willing to bid EV_signal + EV_ordering + EV_builder. Where EV_builder = the increase in block win probability * builder strategy profit, i.e., the change in the expected value of the block if the order on auction is exclusive to one builder. We can see this is larger than what a normal searcher is willing to bid. [33] Further reading on this in the excellent paper by Gupta et. al 2023 [34].
So, BOFAs have the potential to result in higher auction revenues and rebates to the user, but whether they are able to generate more welfare will remain up to question as the market becomes more concentrated and the potential for rent extraction increases. While there are currently no BOFAs released, we expect this architecture to be deployed in the future, especially as builder searchers continue to have a dominant position in the block-building market.
Conclusions on OFA design
The previous analysis illuminates the difficulty of successful mechanism design. While OFAs might initially seem like a simple design, we hope it is clear from this chapter that designing OFAs is all but that. This endeavour requires a team with a sophisticated command of auction, game and blockchain theory. Teams need to thoroughly evaluate the design choices they have made and understand and be comfortable with the trade-offs that they imply. While building around and finding out might have been a valid way to build protocols when crypto and DeFi were much more nascent, when operating in naturally adversarial environments with profit-motivated participants, we must ensure that designs are made with a solid understanding of their implications.
We can choose to seek short-term efficiency and build systems that only work when limited to a known group of participants or we can build systems that do not instate a winning class due to barriers to entry. There might be a price that we pay in efficiency, but the ethos of Ethereum is not to value efficiency over all other goals – otherwise, we might as well run everything on Binance’s servers.
The Order Flow Auction landscape
These inherent difficulties have not deterred teams from building solutions to monetize users’ order flow. There has been a significant amount of venture capital deployed to teams building dedicated OFA solutions and in addition to this, major investments have also been made by existing teams expanding their product scope to include OFA solutions.
Let’s recall our earlier definition of OFAs – it is a mechanism for order flow originators or users to be compensated for the value that their intents contain by forcing sophisticated third parties to compete in an auction for exclusive execution rights.
We identified at least 27 solutions in public that fit this description: 1inch Fusion, Anoma, Aperture Finance, API3 OEV, Blink, BackRunMe, Brink, CoWSwap, DFlow, Essential, Flood, Fastlane Atlas, Hashflow, Kolibrio, Matcha, Memswap, Merkle, MEV-Blocker, MEV-Share, MEVWallet, Nectar, OpenMEV, PropellerHeads, Skip, SUAVE, UniswapX, and Wallchain.
This frenzy of solutions has also translated into real changes in the transaction supply chain. Recall from earlier that Blocknative data shows nearly 15% of all transactions on Ethereum are now bypassing the normal mempool and going through OFAs and private RPCs.
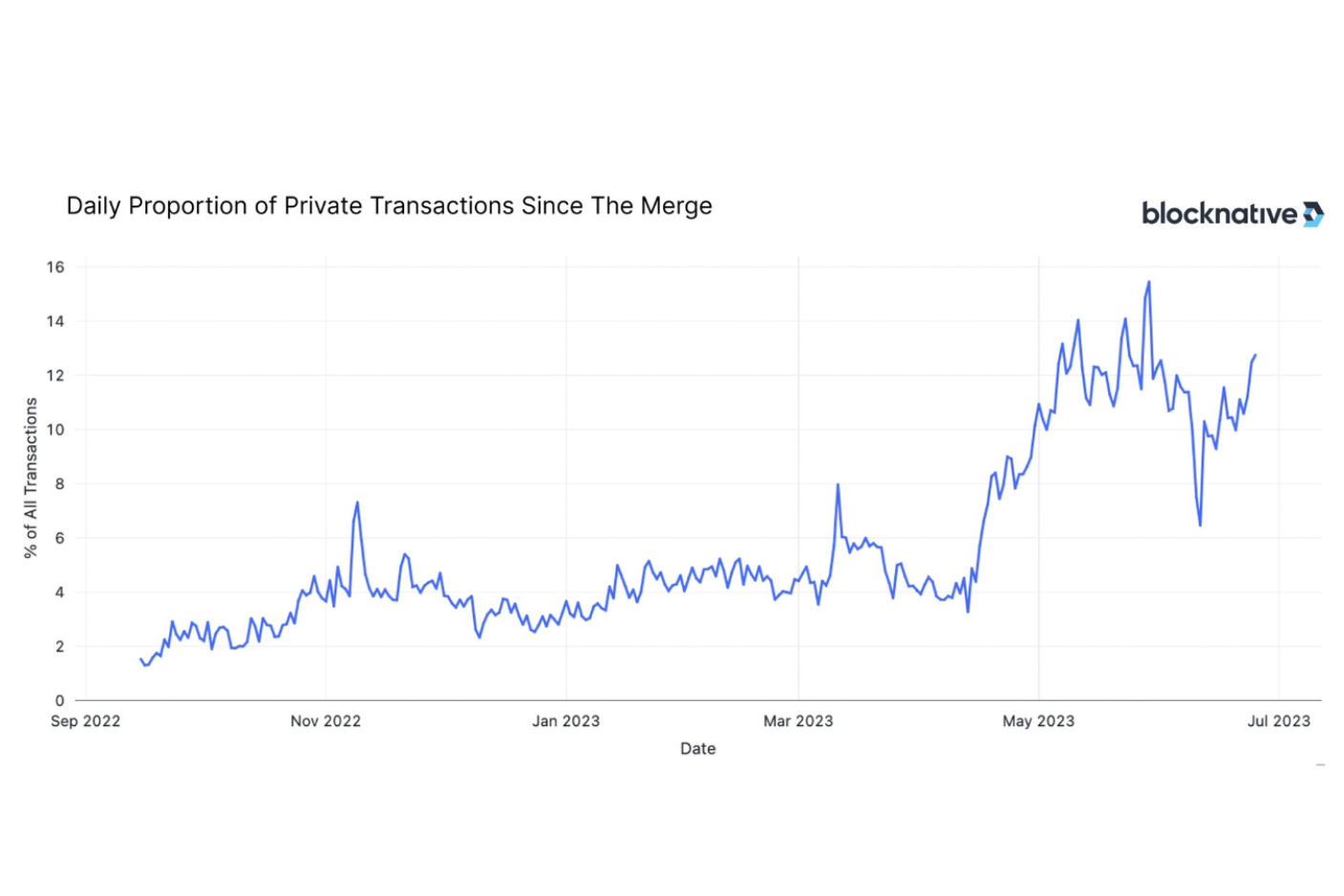
There are many different ways we could formulate a categorization from the previously specified design dimensions. Coming up with a mutually exclusive and completely exhaustive categorization for all OFAs is difficult because even seemingly small changes in OFA design can result in large differences in how an OFA works.
We have chosen to focus on two important axes:
- 1. Auction generality: General vs. Specialized
- 2. Order types: Transactions vs. Intents
This gives us the following four types of auctions:
- 1. General transaction-based auctions
- 2. Specialized transaction-based auctions
- 3. Specialized intent-based auctions
- 4. General intent-based auctions
The following market map looks at the major released OFAs based on this segmentation into general/specialized, transaction/intent-based auctions:
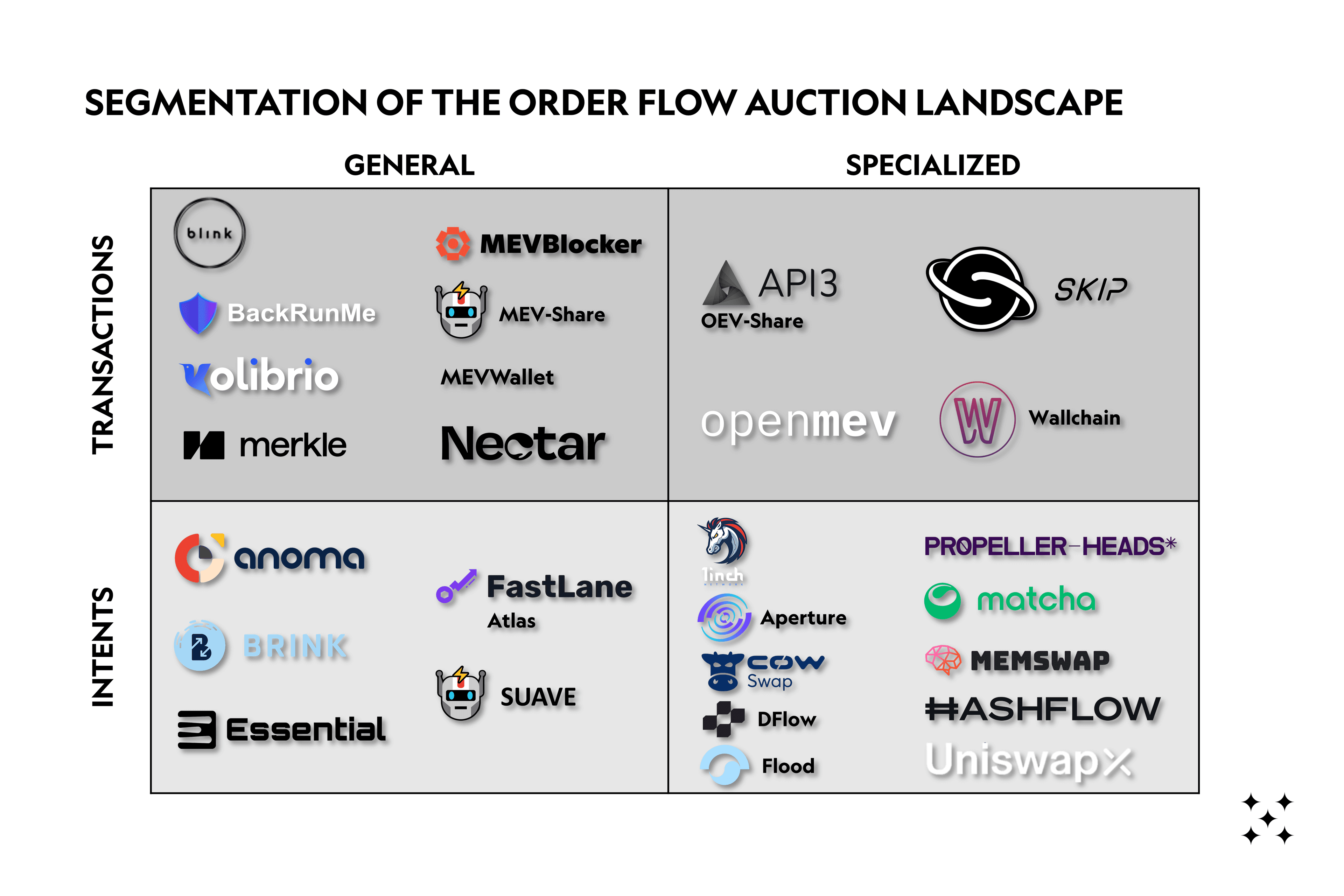
1. General transaction-based auctions
General transaction-based auctions sell access to signed transactions which interact with all types of on-chain applications (DEXes, DeFi protocols, Oracles, etc.).
Most of the currently operating OFAs are of this type, which is explained by three main factors:
- 1. The auction infrastructure is relatively simple to implement. The OFA just needs to collect user transactions (usually via a public RPC endpoint), strip them of their signature and put them up for auction, giving the winner of the auction the full transaction with the signature and thus the exclusive right to execute. After the winner has been selected, the searcher’s bundle is sent to one or more block builders for inclusion in the next block.
- 2. By not limiting the types of transactions that can be put on sale, the OFA aims to maximize their potential market.
- 3. As we know from the previous section, auction revenues benefit from the complementarity of order flow.
While these types of auctions are easier to implement than intent-based ones, a major downside is the fact that users cannot be compensated for their order flow implicitly, with better execution. As discussed before, since the computational path is already set, the winner of the auction cannot change, for example, the order routing of a swap to make it more efficient.
Instead, these OFAs usually compensate the user by paying some share of the auction revenues (i.e., the MEV the transaction contains) to the originator with an on-chain transaction. Other models for compensation, like token-based rebates or gas payments, exist as well.
Currently, the OFAs that can be classified under this architecture are the following: Blink, BackRunMe, Kolibrio, Merkle, MEV-Blocker, MEV-Share, MEV-Wallet, and Nectar.
2. Specialized transaction-based auctions
Specialized transaction-based auctions sell rights of execution to transactions coming from specific applications.
Going back to the history of OFAs, we notice that the first released OFAs were of this type, focusing on providing DEX traders with gas-free trades or cash-back. This makes sense considering that MEV was mostly associated with (and still mostly is) DEX trading.
Because these applications are application specific, they do not need to rely only on the user changing the RPC provider of their wallet. In addition, they can directly integrate with the application to capture the MEV from the user's transactions. This can be beneficial in bridging the adoption gap with OFAs, since benefitting from rebates might not require any user behaviour change.
Deployed OFAs that can be classified under this category are API3 OEV, Skip’s OFA, OpenMEV (SushiGuard), and Wallchain.
3. Specialized intent-based auctions
In specialized intent-based auctions, users expose their use-case specific (e.g. token swapping, lending) intents to specialized third parties, who come up with a solution to the user’s wishes, a set of transactions that achieve the user’s intent within the parameters provided. This explains a commonly used name for these third parties, solvers.
One of the main benefits of these types of auctions is that being intent-based means the auction can select the winner based on execution improvement instead of how much the bidder is willing to pay as a rebate. Execution improvement can be in the form of better order routing or a market maker providing better quotes than what is available on the market, for example.
In addition to this, short-term specialized auctions are easier to implement and integrate with, as the third parties responsible for execution can specialize in one specific type of intent, like a token swap. The more general the auction gets, the more complex it will be for third parties to find the optimal way to execute user orders, which likely means that execution will suffer.
Currently, the only projects that fit under this categorization are swap-specific protocols, where users’ intents to trade are sent to third parties, either solvers or market makers, who use different off-chain or on-chain liquidity sources to fulfil the order at the best possible price. Given that most of MEV today is caused by DEX trades, an app-specific approach, focused on filling users’ trades, is not a bad solution in the short term. We expect that other types of app-specific intent use cases will emerge as the space matures, for example in NFT trading or bridging.
All of the currently released intent-based auctions allow only permissioned actors to execute user intents. This is because relative to transaction-based systems, users have to put a lot more trust in the solvers in intent-based auctions. This is because the user gives relatively free reign for the solver to formulate transactions that achieve their intent. To protect users from malicious solvers, protocols like CoWswap require the solvers to bond a significant amount of value that can be slashed and paid back to victims in case of malicious or unintended behaviour.
Currently announced/released app-specific intent protocols are 1inch Fusion, Aperture Finance, CoWSwap DFlow, Flood, PropellerHeads, Matcha, MemSwap, HashFlow, UniswapX.
4. General intent-based auctions
General intent-based auctions seem like the holy grail of OFA design. In a perfect world, all order flow would go through one trust-minimized, fully robust, composable, and user welfare maximizing OFA, whose orders are intents. This would allow us to maximize synergies of order flow, optimize for user execution and avoid market fragmentation.
Whether this world is feasible without making significant trade-offs is a separate question. There are significant barriers to achieving an auction that would be able to process all kinds of user intents.
Flashbots, with SUAVE, is one of the most prominent teams attempting to build out a generalized solution. We can think of SUAVE as a platform on top of which OFAs can be deployed and compete against each other in a permissionless/trust-minimized manner.
One such solution is Fastlane Atlas: a framework for dApps to create their own OFAs, which can be deployed on top of SUAVE as a smart contract.
Other teams that are building in this category are Anoma, Brink and Essential. Anoma is building an architecture for creating intent-based blockchains. Brink & Essential are also creating a protocol for the expression and fulfilment of general intents, and are currently focused on EVM chains.
Conclusion
In this report, we covered the past, present and future of Order Flow Auctions.
We have seen how addressing the negative externalities of MEV extraction is an existential question for the whole on-chain economy.
While addressing MEV at the application layer might be desirable, it often requires user behaviour change. Due to user stickiness and general unawareness about MEV, application-level mitigation seems like a solution that is only viable in the long term. It is also likely that even if application/infra-level MEV mitigation is successful, there will always remain some residual MEV that can be redistributed.
OFAs are an attractive solution in the short- to medium-term because they provide a way to mitigate MEV without requiring significant user behaviour change. OFAs are not a monolith, there are a plethora of designs, that optimize the user experience in different ways.
In the future, OFAs, especially intent-based solutions, can contribute to further centralization of the MEV supply chain. It is imperative for us to ensure that MEV mitigation does not completely compromise the fundamental values underpinning crypto, censorship resistance & permissionlessness.
Thank you to Mike Neuder, Danning Sui, Uri Klarman, 0xTaker, Jannik Luhn, Greg Vardy, Eduardo Carvalho, Alex Watts, Barry Plunkett, Maghnus Mareneck & the CoWswap team for your valuable feedback.
Footnotes
- 1.
95-99% of the MEV available in the most competitive public opportunities, like liquidations and atomic DEX arbitrage
- 2.
Originally presented in the excellent Frontier Tech post “The Order Flow Auction Design Space”: https://frontier.tech/the-orderflow-auction-design-space
- 3.
Note that this also refers to validators not running MEV-boost but building blocks on their own, although no practical examples of validators integrating with OFAs exist currently.
- 4.
"Payment for Order Flow", 1993, SEC
- 5.
Flow Toxicity and Liquidity in a High Frequency World, Easley, Lopez de Prado, & O'Hara, 2023
- 6.
Payment for Order Flow and Price Improvement, Levy, 2022
- 7.
Payment For Order Flow, CFA Institute, 2016
- 8.
Just-In-Time Liquidity on the Uniswap Protocol, Wan & Adams
- 9.
- 10.
The Future of MEV is SUAVE, Flashbots, 2022
- 11.
Tweet, Blocknative
- 12.
MEV Outlook 2023, EigenPhi, 2023
- 13.
A new game in town, Frontier Research, 2023
- 14.
Note that these are back-of-the-envelope estimates using the two referenced articles. The main point is to illustrate the relative sizes between arbitrage vs. non-arbitrage MEV, not the exact figures which are hard to estimate.
- 15.
Automated Market Making and Loss-Versus-Rebalancing, Milionis et. al 2022
- 16.
Automated Market Making and Arbitrage Profits in the Presence of Fees, Milionis et al, 2023
- 17.
Arbitrage loss and how to fix it, PropellerHeads, 2023
- 18.
Probabilistic Approach to MEV-aware DEX Design, Bandeali, 2023
- 19.
A New Game In Town, Frontier Research, 2023
- 20.
EV = Extractable Value
- 21.
One could argue that our hope, in this case, is trying to incorporate as much of this external information on the blockchain as possible therefore turning EV_signal to EV_ordering.
- 22.
There's an interesting question here about why we have been exposed to so much MEV in the first place; some of the most popular application and protocol-level designs were made when the dark forest of MEV was not yet illuminated. Nowadays, application developers ignore their protocols MEV exposure at their own risk. Testing in production does not work as well when there are teams of profit-driven on-chain prodigies ready to take advantage of every suboptimal design choice.
- 23.
Coined in the Flash Boys 2.0 paper
- 24.
Selling Spectrum Rights, McMillan, 1994
- 25.
Further reading: FRP-20:An Initial Approach to Order Flow Auction Design, Garmidi, 2022
- 26.
Order Flow Auction Treasure Map, Kilbourn, 2023
- 27.
What Is the National Best Bid and Offer (NBBO)?, Hayes, 2022
- 28.
From auctions.google.com to auctions.best, Chitra, 2023
- 29.
Censorship Resistance in On-Chain Auctions, Fox, Pai, & Resnick, 2023
- 30.
- 31.
Fair Market Principles, Flashbots
- 32.
- 33.
Note that this also applies in SOFAs where block builders can bid and send the bundle only to their builder, but to our knowledge, the only example was Rook, which is no longer in operation. In fact, these auctions would likely eventually become BOFAs, as only searcher-builders would be competitive in such an auction in the medium- to long-term.
- 34.
The Centralizing Effects of Private Order Flow on Proposer-Builder Separation, Gupta, Pai, Resnick, 2023